แผนภูมิ Smith: ประวัติความเป็นมาและเหตุใดจึงสำคัญสำหรับนักออกแบบ RF

นักออกแบบมือใหม่ที่ทำการออกแบบ RF และพยายามทำการเชื่อมต่อโดยตรงระหว่างสองส่วนประกอบ—เช่น จากออสซิลเลเตอร์ที่ควบคุมด้วยแรงดันไฟฟ้า (VCO) ไปจนถึงมิกเซอร์—ต้องพบกับกราฟวงกลมที่แปลกประหลาดบนแผ่นข้อมูลส่วนประกอบอย่างไม่ต้องสงสัย เช่น สิ่งเหล่านี้สำหรับ Maxim Integrated MAX2472ตัวขยายสัญญาณบัฟเฟอร์ 500 ถึง 2500 megahertz (MHz) VCO (รูปที่ 1) กราฟเหล่านี้เรียกว่าแผนภูมิ Smith แตกต่างจากที่เห็นในวิชาพีชคณิตหรือสถิติอย่างมาก โดยไม่ต้องสงสัย

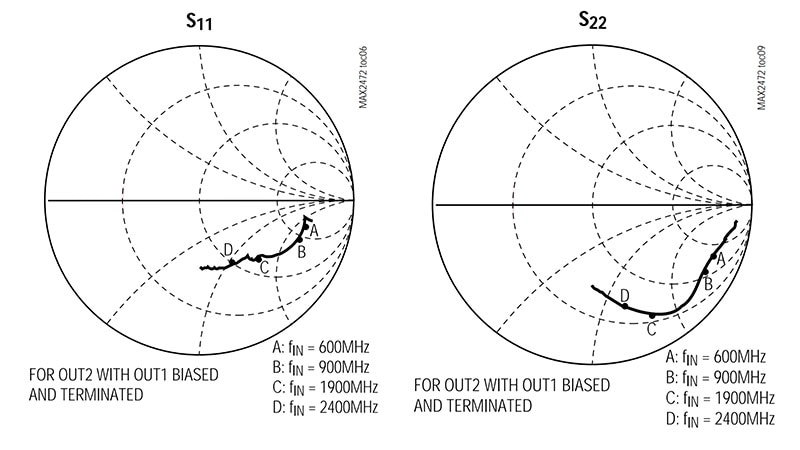รูปที่ 1: แผ่นข้อมูลส่วนประกอบ RF จำนวนมากรวมถึงแผนภูมิ Smith ที่แสดงค่าของพารามิเตอร์หลักที่ความถี่การทำงานที่แตกต่างกัน เช่น ค่าเหล่านี้สำหรับแอมพลิฟายเออร์บัฟเฟอร์ Maxim MAX2472 VCO ที่ 600, 900, 1900 และ 2400 MHz (แหล่งรูปภาพ: Maxim Integrated)

แผนภูมินี้ตั้งชื่อตามชื่อ Phillip Smith วิศวกรของ Bell Telephone Laboratories ซึ่งคิดค้นและปรับแต่งแผนภูมิระหว่างปี 1936 และ 1939 ขณะที่ทำงานเพื่อทำความเข้าใจสายส่งและคลื่นนิ่งที่ความถี่สูงในตอนนั้นที่ 1 MHz (เรียกว่า megacycles ต่อวินาทีในสมัยนั้น) แผนภูมิวงกลมที่ดูแปลกตาของเขาได้กลายเป็นเครื่องมือที่มีประโยชน์และทรงพลังที่สุดเพียงเครื่องมือเดียวสำหรับการทำงานและปรับวงจรความถี่สูงให้เหมาะสมโดยคำนึงถึงอิมพีแดนซ์อินพุตและเอาต์พุต แม้ในยุคของคอมพิวเตอร์ที่ทรงพลังและเครื่องมือออกแบบโดยใช้คอมพิวเตอร์ช่วย (CAD)

ในบรรดาการใช้งานหลาย ๆ อย่าง แผนภูมิ Smith เป็นวิธีที่มีประสิทธิภาพในการแสดงภาพตัวเลือกการออกแบบเมื่อพยายามจับคู่แหล่งที่มาระหว่างสเตจและอิมพีแดนซ์ของโหลด ซึ่งเป็นข้อพิจารณาที่สำคัญมากในหลายวงจร โดยเฉพาะการออกแบบ RF มีเหตุผลสองประการที่การจับคู่ดังกล่าวมีความสำคัญ:

• ประการแรก เพื่อให้เกิดการถ่ายโอนกำลังสูงสุดจากแหล่งหนึ่งไปยังโหลด ซึ่งก็คืออิมพีแดนซ์เชิงซ้อนของแหล่งกำเนิด R_S + jX_S จะต้องเท่ากับคอนจูเกตเชิงซ้อน R_L - jX_L ของอิมพีแดนซ์ของโหลด:

เมื่อ R คือส่วนความต้านทาน (จริง) ของอิมพีแดนซ์และ X คือส่วนปฏิกิริยา (อุปนัยหรือตัวเก็บประจุ) (รูปที่ 2)

รูปที่ 2: ความท้าทายที่สำคัญในการออกแบบ RF และสายส่งคือการทำให้มั่นใจว่าแหล่งกำเนิด "เห็น" อิมพีแดนซ์โหลด ซึ่งเป็นคอนจูเกตเชิงซ้อนของอิมพีแดนซ์ของแหล่งกำเนิด แม้ว่าอิมพีแดนซ์โหลดนั้นจะไม่อยู่ที่นั่นก็ตาม (แหล่งรูปภาพ: HandsOnRF.com)

• ประการที่สอง แม้ว่าการสูญเสียพลังงานดังกล่าวจะไม่เป็นปัญหา (แม้ว่าจะเกือบทุกครั้งก็ตาม) จำเป็นต้องมีการจับคู่อิมพีแดนซ์เพื่อลดการสะท้อนของพลังงานจากโหลดกลับไปยังแหล่งกำเนิด ซึ่งอาจทำให้วงจรเอาท์พุทของแหล่งจ่ายเสียหายได้

สิ่งที่แผนภูมิ Smith แสดง

แผนภูมิ Smith เป็นแผนภาพเชิงขั้วของสัมประสิทธิ์การสะท้อนเชิงซ้อน (เรียกอีกอย่างว่าแกมมาและแสดงโดย rho (Γ)) มันประสบความสำเร็จในการแสดงสิ่งที่อาจดูเหมือนเป็นงานที่แทบจะเป็นไปไม่ได้ในตอนแรก: การทำกราฟพร้อมกันของส่วนจริงและจินตภาพของอิมพีแดนซ์เชิงซ้อน โดยที่ส่วนจริง R สามารถอยู่ในช่วงตั้งแต่ 0 ถึงอนันต์ (∞) และส่วนจินตภาพ X สามารถ สแปนลบอนันต์ถึงบวกอินฟินิตี้—และทั้งหมดนี้ถูกทำบนกระดาษแผ่นเดียว

แผนภูมิ Smith แบบง่าย ซึ่งแสดงวงกลมของความต้านทานคงที่และส่วนโค้งของค่ารีแอกแตนซ์คงที่ เป็นจุดเริ่มต้นที่ดีในการทำความเข้าใจการจัดเรียง (รูปที่ 3) เพื่อประโยชน์เพิ่มเติม แผนภูมิยังให้วิธีการแสดงพารามิเตอร์การกระเจิง (s-parameters) และความสัมพันธ์ของค่ากับการวัดและการพิจารณาฮาร์ดแวร์จริง

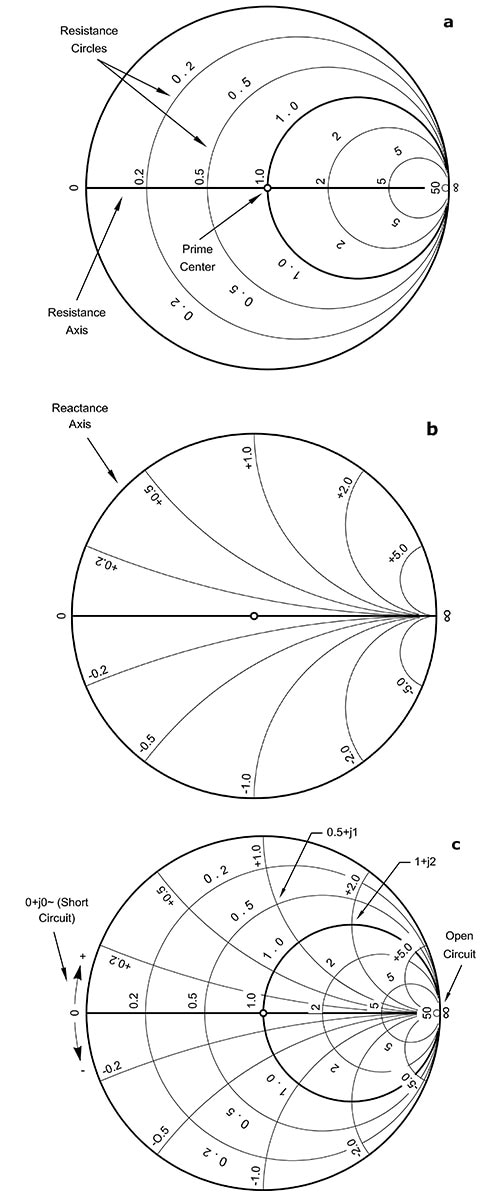รูปที่ 3: แผนภูมิ Smith แสดงส่วนโค้งของความต้านทานคงที่ (a) และวงกลมของค่ารีแอกแตนซ์คงที่ (b) ซึ่งถูกรวมและซ้อนทับ (c) เพื่อให้มุมมองที่เป็นไปได้ของอิมพีแดนซ์ทั้งหมด (แหล่งรูปภาพ: ARRL.org)

เมื่อค่าอิมพีแดนซ์เชิงซ้อนเหล่านี้ถูกทำเครื่องหมายบนแผนภูมิ Smith แล้ว แผนภูมิสามารถใช้เพื่อระบุพารามิเตอร์ต่าง ๆ ที่มีความสำคัญต่อการทำความเข้าใจเส้นทางสัญญาณ RF หรือสถานการณ์ของสายส่ง ได้แก่:

• ค่าสัมประสิทธิ์การสะท้อนของแรงดันและกระแสสลับเชิงซ้อน
• ค่าสัมประสิทธิ์การส่งกระแสสลับและแรงดันเชิงซ้อน
• ค่าสัมประสิทธิ์การสะท้อนกำลังและการส่งกำลัง
• การสูญเสียเนื่องจากการสะท้อน
• การสูญเสียเนื่องจากการย้อนกลับ
• ปัจจัยการสูญเสียคลื่นนิ่ง
• แรงดันและกระแสสูงสุดและต่ำสุด ตลอดจนอัตราส่วนคลื่นนิ่ง (SWR)
• รูปร่าง ตำแหน่ง และการกระจายเฟสพร้อมกับแรงดันและคลื่นนิ่งในปัจจุบัน

แต่นั่นเป็นเพียงส่วนหนึ่งของพลังของแผนภูมิ Smith แม้ว่าจะเป็นประโยชน์และบ่อยครั้งที่นักออกแบบจำเป็นต้องรู้พารามิเตอร์ข้างต้น แผนภูมิ Smith สามารถใช้เป็นแนวทางในการวิเคราะห์และตัดสินใจออกแบบได้ ซึ่งรวมถึง:

• การแสดงอิมพีแดนซ์เชิงซ้อนกับความถี่
• การแสดงพารามิเตอร์ s ของเครือข่ายเทียบกับความถี่
• การประเมินค่ารีแอกแตนซ์อินพุตหรือความไวต่อต้นขั้วแบบเปิดและแบบย่อ
• การประเมินผลกระทบของอิมพีแดนซ์แบบแบ่งและแบบอนุกรมต่ออิมพีแดนซ์ของสายส่ง
• สำหรับการแสดงและประเมินลักษณะอิมพีแดนซ์อินพุตของต้นขั้วเรโซแนนซ์และแอนตี้-เรโซแนนซ์ รวมถึงแบนด์วิดท์และ Q
• การออกแบบเครือข่ายที่จับคู่อิมพีแดนซ์โดยใช้สตับแบบเปิดหรือชอร์ตแบบเดี่ยวหรือหลายแบบ ส่วนของเส้นควอเตอร์เวฟ และส่วนประกอบ LC แบบรวมเป็นก้อน

ประโยชน์ของแผนภูมิ Smith

เมื่อมองแวบแรก แผนภูมิ Smith แบบมาตรฐานที่มีรายละเอียดครบถ้วนอาจดูเหมือนเส้นที่สับสนจนแทบจะเข้าใจยากไปในทุกทิศทาง (รูปที่ 4) แต่จริงๆ แล้วเป็นเพียงการแสดงภาพที่มีความละเอียดสูงกว่าและมีรายละเอียดมากขึ้นของแผนภูมิแบบง่ายที่แสดงไว้ก่อนหน้านี้ คุณสามารถ ดาวน์โหลดฉบับที่ปริ๊นต์ได้ ของแผนภูมิ Smith จากแหล่งข้อมูลออนไลน์ DigiKey Innovation Handbook

รูปที่ 4: แผนภูมิ Smith ทั่วไปอาจดูยิ่งใหญ่ แต่นั่นเป็นเพียงการแสดงผลที่มีความละเอียดสูงและมีรายละเอียดมากขึ้นของแผนภูมิแบบง่ายที่แสดงไว้ก่อนหน้านี้ (แหล่งรูปภาพ: DigiKey)

แผนภูมิ Smith แสดงมากกว่าโซลูชันเดียวสำหรับปัญหาที่เกี่ยวข้องกับการออกแบบจำนวนมาก โดยแสดงวิธีแก้ปัญหาที่เป็นไปได้มากมาย นักออกแบบสามารถตัดสินใจได้ว่าชุดใดเสนอชุดค่าส่วนประกอบที่เหมาะสมสำหรับสถานการณ์เฉพาะ เช่น ค่าที่ใช้งานได้จริงสำหรับตัวเหนี่ยวนำและตัวเก็บประจุที่จับคู่อิมพีแดนซ์ ในกรณีส่วนใหญ่ มาตราส่วนตัวเลขของแผนภูมิจะเป็นระบบ "ทำให้เป็นมาตรฐาน" ถึง 50 โอห์ม (Ω) เนื่องจากเป็นอิมพีแดนซ์ที่ใช้บ่อยที่สุดในการออกแบบ RF

แผนภูมิ Smith มีความสำคัญและมีประโยชน์มากจนเครื่องมือทดสอบจำนวนมากสำหรับแอปพลิเคชัน RF และไมโครเวฟ เช่น เครื่องวิเคราะห์เครือข่ายเวกเตอร์ (VNA) สามารถจัดทำแผนภูมิและแสดงผลได้ สำหรับตัวอย่าง Teledyne LeCroy T3VNA เป็นโหมดที่ VNA ได้นำเสนอ (Figure 5)

รูปที่ 5: เครื่องวิเคราะห์เครือข่ายเวกเตอร์ T3VNA สามารถแสดงข้อมูลที่ได้มาในรูปแบบแผนภูมิ Smith (แหล่งรูปภาพ: Teledyne LeCroy)

การเรียนรู้เพื่อใช้งานแผนภูมิ Smith นั้นยากแค่ไหน? เช่นเดียวกับคำถามส่วนใหญ่ เหมือนกับการถามนักเรียนแต่ละคนว่าพวกเขารู้สึกอย่างไรเกี่ยวกับความยากของแคลคูลัสหรือทฤษฎีสนามแม่เหล็กไฟฟ้า ซึ่งก็แล้วแต่ มีบทเรียนแบบข้อความและวิดีโอออนไลน์มากมายที่เริ่มต้นด้วยพื้นฐานแผนภูมิ Smith จากนั้นจึงเพิ่มสมการของสายส่งและมุมมองการวิเคราะห์ พวกเขายังต้องพบกับตัวอย่างมากมายเพื่อที่จะใช้งานมันให้ได้ แน่นอนว่ายังมีแอปและโปรแกรมที่ช่วยอำนวยความสะดวกในการสร้างกราฟ กำหนดกรอบปัญหา และประเมินตัวเลือกโดยใช้แผนภูมิ Smith อย่างไรก็ตาม การทำความเข้าใจพื้นฐานของแผนภูมิก่อนจะใช้วิธีเหล่านี้จะช่วยให้เข้าใจได้ดีขึ้น

บทสรุป

เป็นเรื่องมหัศจรรย์ที่เครื่องมือกราฟิกที่พัฒนาขึ้นเมื่อกว่า 80 ปีที่แล้ว นานก่อนการออกแบบ RF ที่เรารู้อยู่แล้วว่ามันมีอยู่จริง ยังคงเป็นหนึ่งในแหล่งข้อมูลหลักสำหรับความท้าทายในการออกแบบ RF ทั้งบนกระดาษและซอฟต์แวร์ ในการใช้งานทั้งสองวิธี แผนภูมิ Smith เป็นเครื่องมือที่มีประสิทธิภาพสำหรับการแสดงและประเมินพารามิเตอร์ RF และรับข้อมูลเชิงลึกเกี่ยวกับทางเลือกการออกแบบและการชั่งน้ำหนักกับปัจจัยอื่นที่เกี่ยวข้อง วิธีที่ดีที่สุดที่จะเรียนรู้เกี่ยวกับพลังของแผนภูมิ Smith และสิ่งที่แผนภูมิสามารถทำประโยชน์ให้คุณได้ก็คือใช้งานแผนภูมิและใช้งานมันผ่านตัวอย่างจำนวนมากที่เผยแพร่อยู่ทั่วไป

บทความแนะนำ

1 – “The Smith Chart: เครื่องมือกราฟิก 'โบราณ' ยังคงมีความสำคัญในการออกแบบ RF”

https://www.digikey.com/en/articles/the-smith-chart-an-ancient-graphical-tool-still-vital-in-rf-design

2 – “SAW ผลิตภัณฑ์กู้ภัยตัวกรองไร้สาย จากการใช้งานที่ไม่ต่อเนื่องที่ใช้งานจริงไม่ได้”

https://www.digikey.com/en/articles/saw-filters-rescue-wireless-products-from-impractical-discrete-implementations

3 – “ทำความเข้าใจพื้นฐานของตัวขยายสัญญาณรบกวนต่ำและกำลังสูงในการออกแบบไร้สาย”

https://www.digikey.com/en/articles/understanding-the-basics-of-low-noise-and-power-amplifiers-in-wireless-designs

4 – “ใช้ Log Amps เพื่อเพิ่มความไวและประสิทธิภาพใน Wide-Dynamic-Range RF และ Optical Links”

https://www.digikey.com/en/articles/use-log-amps-to-enhance-sensitivity-logarithmic-amplifiers